SUR QUELQUES CLASSES DE PROCESSUS ALEATOIRES NON STATIONNAIRES
Keywords:
processus aléatoire non stationnaire, fonction de corrélation, représentation intégrale, décomposition spectrale d'un opérateur auto-adjointAbstract
Dans ce travail, on obtient des représentations intégrales pour certains processus aléatoires de second ordre non stationnaires ainsi que pour leurs fonctions de corrélation. Ces représentations sont analogues à celles connues dans le cas des processus aléatoires stationnaires. Les processus que nous considérons sont solutions du problème de Cauchy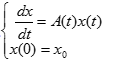
, où A(t) est, pour tout t Î [0,T], un opérateur linéaire borné dans l'espace de Hilbert généré par le processus x(t) et la fonction de corrélation K(t,s) vérifie une certaine équation aux dérivées partielles. Ces classes de processus généralisent la classe des processus aléatoires stationnaires. En effet, dans ce cas, il suffit de prendre A(t) = A, où A est auto-adjoint et la fonction de corrélation K(t,s) vérifie l'EDP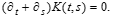 
Downloads
References
- Livschits M.S, Yancevich A.A., "Operators colligations in Hilbert spaces", Willey (1979).
- Abbaoui L., "Application de la théorie spectrale des systèmes d'opérateurs linéaires non auto adjoints à l'étude des champs aléatoires non homogènes", Thèse de doctorat, Kharkov, (1984).
- Abbaoui L., "A class of inhomogeneous random fields", Vestnik Khar'kov. Gos. Univ. N° 254, (1984) (en russe).
- Abbaoui L., Yancevich A.A., "Quelques classes de champs aléatoires non homogènes", Publications de l'Institut Ukrainien de la Recherche Scientifique, N°2206 (1984).
- Zolotarev V.A., Yancevich A.A., "Nonstationary curves in Hilbert spaces and nonlinear operator equations. Theory of operators, subharmonic functions", Naukova Dumka, Kiev, 1991, pp. 54-60 (Russian).
- Kirchev K.P., Zolotarev V.A., "Nonstationary curves in Hilbert spaces and their correlation functions II", Journal of Intger. Equat. Oper. Th., Vol.19, Birkhauser verlag, Basel, (1994), pp. 447-457.
- Abbaoui L., "Sur quelques transformations linéaires des champs aléatoires homogènes", Maghreb Math. Rev., Vol. 4, N°1, June (1995), pp. 1-8.
- Riesz F., Nagy B. Sz., "Functional Analysis", Ungar, New York, (1955).
- Guikhman I., Skorokhod A., "Introduction à la théorie des processus aléatoires", éditions Mir, Moscou, (1980).
- Ibrahimov I, Rozanov Y., "Processus aléatoires gaussiens", éditions Mir, Moscou, (1974).
