SUR LES OPERATEURS SOUS-LINEAIRES p-SOMMANTS
Mots-clés :
Espace réticulé, opérateur sous-linéaire, opérateurs p-sommantsRésumé
Soit T un opérateur sous-linéaire borné entre X espace de Banach et Y espace de Banach complètement réticulé, et ∇T l'ensemble des opérateurs linéaires bornés <=T. On va montrer que s'il existe un filtre d'opérateurs {Ui}iϵI ⊂ ∇T et C > 0 tels que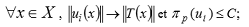 
, et il y a équivalence entre T, p-sommant et u, p-sommant, pour tout u dans ∇T.
Téléchargements
Références
- Pietsch A., Absolut p-summierende in Abbildungen in normierten Räumen, Studia Math., 28 (1967), pp. 333-353.
- Pietsch A., Operator ideals, North-Holland, Amsterdam (1978).
- Krivine J.L., Théorème de factorisation dans les espaces réticulés, Séminaire Maurey-Schwartz, 1974-1975, exposé n°XXII et XXIII.
- Lindenstrauss J. and Tzafriri L., Classical Banach spaces, Springer-Verlag, Berlin Heidelberg (1996).
- de la Barrière R.P., Convex Analysis, Vector and Set-Valued Measures, Publication de l'Université Paris VI, n°33, (1980).
- Pisier G., Factorization of linears operators and the geometry of Banach spaces, CBMS (Regional conferences of the AMS) 60, (1986), Rep. with corrections 1987.
- Schwartz L., Geometry and Probability in Banch spaces, Lectures Notes in Mathematics n°852, Springer-Verlag, Berlin, Heidelberg, New-York.
- Kadison N., A representation theory for commutative topological algebra, Mem. Amer. Math. Soc., 17.
- Grothendieck A., Résumé de la théorie métrique des produits tensoriels topologiques, Bol. Soc. Math. Sao Paulo, (1956).
- Rietz R., A proof of the Grothendieck inequality, Israël, J. Math., 19, (1974), pp. 271-276.
